Понятия и определения

Целые (натуральные) числа

Первые представления о числе приобретены людьми в незапамятной древности. Они возникли из счета людей, животных, плодов, различных изделий человека и других предметов. Результатом счета являются числа Один, Два, Три и т.д. Эти числа носят название — натуральные числа. В арифметике их также называют — целые числа.
Понятие о натуральном числе является одним из простейших понятий. Его можно пояснить только предметным показом.
Евклид (III век до нашей эры) определял натуральное число как множество, составленное из единиц. Такого рода определения можно найти и во многих нынешних учебниках. Но слово множество или совокупность совсем не понятнее слова число.
Ряд целых чисел

1.	1, 2, 3, 4, 5, ...

продолжается без конца. Он носит называние — натуральный ряд

Сложение, сумма

Понятие о том, что такое сложение, возникает из таких простых фактов, что оно не нуждается в определении и не может быть определено формально.

слагаемое+ слагаемое= сумма

Например

7+ 2= 9

7 — слагаемое
2 — слагаемое
9 — сумма
 Вычитание, разность

Вычитание — есть нахождение одного из слагаемых по сумме и другому слагаемому. Сумма получает название уменьшаемого, данное слагаемое - вычитаемого, искомое слагаемое — разности.

Уменьшаемое−Вычитаемое= Разность

например

9−5= 4

9 — Уменьшаемое
5 — Вычитаемое
4 — Разность Умножение, произведение

Умножить некоторое число на целое число — значит повторить множимое слагаемое столько раз, сколько указывает множитель. Результат называется произведением.

1	множитель × 2 множитель= произведение

Например

3 × 4= 12

Или еще записывают так

3 · 4= 12

3 — Множитель
4 — Множитель
12 — Произведение

а вычисляется так

3 × 4= 3+ 3+ 3+ 3= 12

Чётные и нечётные числа

Четные числа — это такие числа которые делятся на 2 нацело.

Нечетные числа — это такие числа которые не делятся на 2 нацело.

Признаки делимости  Признак делимости на 2 Число делится на два, если его последняя цифра четная или нуль. В остальных случаях — не делится. Например: Число 52 738 делится на 2 так, как последняя цифра 8 — четная. 7 691 не делится на 2, так 1 — цифра нечетная. 1 250 делится на 2, так как последняя цифра нуль. Признаки делимости на 3 На 3 делятся только те числа, у которых сумма цифр делится на 3 Например: Число 17 835 делится на 3, так как сумма его цифр 1. 1+ 7+ 8+ 3+ 5= 24 делится на 3.  Признак делимости на 5 На 5 делятся числа, последняя цифра которых 0 или 5. Другие — не делятся. Пример: 240 делится на 5 (последняя цифра 0). 554 не делится на 5 (последняя цифра 4). Разложение на простые множители Всякое составное число можно единственным способом представить в виде произведения простых множителей. Для разложения на простые множители можно пользоваться следующим правилом: Путь дано число M = 12376. 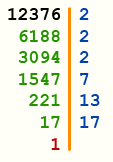Берем по очереди простые числа из соответствующей таблицы. И останавливаемся на том — которое является делителем данного числа M. Проводим вертикальную черту. Слева от нее пишем данное число M. Справа простое число которое является делителем. Второй строкой под данным числом M пишем результат деления. И с результатом деления повторяем все снова. Т.е. ищем в таблице простых чисел — делимое. И так до тех пор пока результатом очередного деления не станет число 1. В результате все числа справа от вертикальной линии — простые множители 12376= 23 · 7 · 13 · 17  Наибольший общий делитель Общий делитель нескольких чисел — это число служащее делителем для каждого из них. Например, Числа 12, 18, 30 имеют общий делитель 3, а так же общий делитель 2. Среди всех общих делителей, всегда есть наибольший. В данном случае для выше перечисленных чисел наибольший общий делитель — это число 6. Для того чтобы найти наибольший общий делитель необходимо разложить каждое из заданных чисел на простые множители. Потом выписать отдельно только те множители которые входят во все заданные числа. Потом перемножаем между собой выписанные числа и результат перемножения и есть наибольший общий делитель. Например, 252= 22 · 32 · 7 441= 32 · 72 1080= 23 · 33 · 5 Наибольший общий делитель НОД (252,441,1080)= 32= 9 Взаимно простые числа Может случиться так, что простых множителей, общих для всех заданных чисел, не будет. Тогда наибольший общий делитель — это число 1. Взаимно простые числа это такие числа наибольший общий делитель которых равен 1. Наименьшее общее кратное Общее кратное нескольких чисел — это число, служащее кратным для каждого из них. Числа 15, 6, 10 имеют общее кратное 180; число 90 — также общее кратное этих чисел. Среди всех общих кратных всегда есть наименьшее, в данном случае число 30. Это число называется наименьшим общим кратным. Чтобы найти наименьшее общее кратное заданных чисел, разлагаем данные числа на простые множители, выписываем все простые множители, входящие хотя бы в одно из данных чисел, каждый из взятых множителей возводим в наибольшую из тех степеней, с которыми он входит в заданные числа. Производим умножение. Например, 252= 22 · 32 · 7 441= 32 · 72 1080= 23 · 33 · 5 Наименьшее общее кратное= 23 · 33 · 5 · 72= 52920 Обыкновенные дроби Обыкновенной дробью (или просто, дробью) называется часть единицы или несколько равных частей (долей) единицы. простые дроби, числитель, знаменатель. Кольцо разделено на 5 секторов. 3 из них красные. Знаменатель дроби — Число, показывающее на сколько долей разделена единица. Числитель дроби — Число, показывающее количество взятых долей. Запись:  3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной. Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному. Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.  Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками. Свойства десятичных дробей.     1.   Десятичная дробь не меняется, если справа добавить нули:                                             13.6 =13.6000.     2.   Десятичная дробь не меняется, если удалить нули, расположенные           в конце десятичной дроби:                                       0.00123000 = 0.00123 . Внимание! Нельзя удалять нули, расположенные не в конце десятичной дроби!    3.    Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести    десятичную точку на одну, две, три и т.д. позиций вправо:                             3.675  --->  367.5 (дробь возросла в 100 раз).    4. Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:                     1536.78 ---> 1.53678 (дробь уменьшилась в 1000 раз). Эти свойства позволяют быстро умножать и делить десятичные дроби на 10, 100, 1000 и т.д. Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом. Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).